Seitdem sich die Mathematik mit Logik beschäftigt, können logische Aussagen nur zwei Werte annehmen - wahr oder falsch. Diese binäre, also zweiwertige Logik entspringt dem wissenschaftlichen Bestreben nach eindeutigen, „scharfen" Aussagen. Eine Aussage der Art „1 + 1 ergibt ungefähr 2" ist für einen Wissenschaftler nicht sehr sinnvoll. Es gibt allerdings Situationen, die von der binären Logik nicht abgebildet werden können. So würde zum Beispiel die Aussage eines Vaters „WENN es am Samstag nicht regnet, DANN besuchen wir einen Vergnügungspark" in der binären Logik schon durch einen einzigen Regentropfen zu langen Gesichtern bei den Kindern führen, da die Aussage „kein Regen" logisch falsch wäre. Ein etwas mehr technisch orientiertes Beispiel ist der Ladezustand eines Akkus. Ein Akku hat nicht nur die Ladezustände „leer" und „voll", sondern beliebig viele Zwischenzustände. Mit einer binärlogischen Beschreibung könnte ein Batterieladegerät nicht arbeiten. Es würde immer um die scharfe Grenze zwischen „leer" und „voll" herumtoggeln und der Akku somit nie einsatzbereit sein.
Mit diesem Problem beschäftigte sich Professor Lofti A. Zadeh von der University of California, Berkeley und entwickelte 1965 seine Theorie der unscharfen Logik - die Fuzzy-Logik. „Fuzzy" kommt aus dem Englischen und bedeutet „unscharf". Die Fuzzy-Logik kennt nicht nur die beiden Aussagen „wahr" und „falsch", sondern auch alle dazwischenliegenden Zustände, wie „etwas", „ungefähr", „ziemlich", etc. So liefert Fuzzy-Logik für obige Beispiele die Ergebnisse „es regnet kaum", worüber sich die Kinder freuen, bzw. „der Akku ist ziemlich voll", worüber sich der Akkubesitzer freut.
Die Unterteilung in beliebig viele Zwischenschritte zwischen „wahr" und „falsch" kommt dem menschlichen Denken näher als die binäre Logik. Dadurch lassen sich technische Zusammenhänge auch von einem in Regelungstechnik unerfahrenem Laien beschreiben und anschließend von einem Regelungstechniker mit nur geringen Kenntnissen der Regelstrecke in eine Fuzzy-Regelung umwandeln. Der Regelungstechniker muß nicht mehr über genaue Kenntnisse der Regelstrecke verfügen, sondern erhält diese über die sprachliche Beschreibung der zu regelnden Anlage.
Prof. Zadeh entwickelte mathematische Modelle, nach denen die sprachlichen Beschreibungen durch mathematische Formeln ausgedrückt werden können. Die Aussage „es regnet" wird als „linguistische Variable" bezeichnet. Sie kann, je nach Regenstärke, „Erfüllungsgrade", auch „Zugehörigkeitswerte" oder „Wahrheitsgrade" genannt, zwischen 0 (entspricht dem binären „falsch") und 1 (entspricht dem binären „wahr") annehmen. Ein Wert von 0,5 bedeutet, daß eine Aussage fuzzylogisch halbwahr ist - die Aussage ist zur Hälfte zutreffend. Linguistische Variablen, wie zum Beispiel die Aussage „es regnet", werden in mehrere genauer spezifizierende Aussagen - den „linguistischen Termen" oder auch „Fuzzy-Sets" - unterteilt. In dem gewählten Beispiel bietet sich die Aufteilung in „es regnet kaum", „es regnet mittel" und „es regnet stark" an. Diese linguistischen Terme überschneiden sich in den meisten Fällen. Der Übergang zwischen schwachem und mittelstarkem Regen ist nicht an einem einzigen Regentropfen auszumachen, sondern vollzieht sich dadurch, daß der Erfüllungsgrad (der Wahrheitsgehalt) des einen Terms langsam abnimmt, wogegen der Erfüllungsgrad des anderen weiter zunimmt.
Jede Regelung hat eine oder mehrere Eingangsgrößen. Diese müssen bei der Fuzzy-Logik in unscharfe Aussagen gewandelt werden. Unscharfe Aussage bedeutet, daß aus einer Eingangsgröße eine Aussage geschlossen wird, die mit einem Wahrheitsgrad zwischen 0 und 1 behaftet ist. So würde zum Beispiel die Eingangsgröße „Körpergröße = 1,60 m" die Aussage „dieser Mensch ist groß" als Schlußfolgerung haben. Diese Schlußfolgerung hätte allerdings einen geringen Wahrheitsgrad. Bei einer Fuzzy-Regelung werden die möglichen Schlußfolgerungen während der Erstellung der Regelung, welche anhand einer sprachlichen Beschreibung der Regelstrecke geschieht, festgelegt. Den Vorgang, die scharfen Eingangsgrößen in „linguistische Variablen" umzusetzen, nennt man „fuzzyfizieren". Bei der „Fuzzyfizierung" wird für jeden realen Wert jedem linguistischen Term ein Erfüllungsgrad zugewiesen. Zum Beispiel würde im Falle der eingangs erwähnten Eingangsgröße „Niederschlagsmenge" für den realen Wert 1,1 der linguistische Term „es regnet kaum" ein Erfüllungsgrad von 0,45, der linguistischen Term „es regnet mittel" ein Erfüllungsgrad von 0,1 und der linguistische Term „es regnet stark" ein Erfüllungsgrad von 0 zugewiesen bekommen. Hat man die Eingangsgrößen fuzzyfiziert, so muß man Regeln in Form von WENN (Ausdruck) DANN (Ergebnis) festlegen. Die Regeln setzen die sprachlichen Beschreibungen der Regelstrecke und ihrer Eigenschaften in ein Fuzzy-"Regelwerk" um. Hierbei ist „Ausdruck" entweder ein linguistischer Term oder eine fuzzylogische Verknüpfung mehrerer linguistischer Terme.
Zu der bereits eingeführten linguistischen Variablen „es regnet" sei die linguistische Variable „es ist warm" hinzugefügt. Diese sei in die drei linguistischen Terme „es ist kühl", „es ist angenehm" und „es ist heiß" unterteilt. Wenn man nun die Entscheidung für oder gegen einen Familienausflug von einem Fuzzy-Regler fällen lassen wollte und die drei Möglichen Aktionen 1) „Wir bleiben Zuhause", 2) „Wir bleiben in der Gegend" und 3) „Wir besuchen einen Vergnügungspark" zur Wahl hätte, so müßte man die folgenden Regeln aufstellen:
| "es regnet" | "es ist warm" | "Ergebnis" | |
| Regel 1 | es regnet kaum | es ist kühl | Aktion 2 |
| Regel 2 | es regnet mittel | es ist kühl | Aktion 1 |
| Regel 3 | es regnet stark | es ist kühl | Aktion 1 |
| Regel 4 | es regnet kaum | es ist angenehm | Aktion 3 |
| Regel 5 | es regnet mittel | es ist angenehm | Aktion 2 |
| Regel 6 | es regnet stark | es ist angenehm | Aktion 1 |
| Regel 7 | es regnet kaum | es ist heiß | Aktion 3 |
| Regel 8 | es regnet mittel | es ist heiß | Aktion 2 |
| Regel 9 | es regnet stark | es ist heiß | Aktion 1 |
Jede dieser Regeln wird nach den vorzugebenden Fuzzy-Verknüpfungsoperatoren ausgewertet und das Ergebnis der Auswertung dem angegebenen Ausgang zugewiesen. Das bedeutet, daß der linguistische Term aus Spalte zwei mit dem linguistischen Term aus Spalte drei mittels eines Fuzzy-Verknüpfungsoperators - zum Beispiel UND - logisch verknüpft wird. Das Ergebnis dieser Verknüpfung ist ein Erfüllungsgrad, der dem Ausgang („Ergebnis") zugewiesen wird. Dabei ist „Ergebnis" wiederum eine linguistische Variable, die in einen oder mehrere linguistische(n) Term(e) unterteilt ist (hier: „Aktion 1" bis „Aktion 4").
Ausgehend von der Annahme, daß es am Tag ein paar Regenschauer gibt und die Temperaturen um 19 Grad Celsius liegen, was hauptsächlich als „es regnet kaum" und „es ist angenehm", aber auch als ein wenig „es regnet mittel" und ein wenig „es ist kühl" eingestuft würde, wären folgende Regeln (hier mit den dazugehörigen Erfüllungsgraden angegeben) erfüllt:
| Linguistische Variable "Regen" | Verknüpfungsoperator | Linguistische Variable "Temperatur" | Ergebnis | |
| Regel 1 | es regnet kaum (0.9) | UND | es ist kühl (0.1) | Aktion 1 (0.1) |
| Regel 2 | es regnet mittel (0.2) | UND | es ist kühl (0.1) | Aktion 2 (0.1) |
| Regel 3 | es regnet kaum (0.9) | UND | es ist angenehm (0.9) | Aktion 3 (0.9) |
| Regel 4 | es regnet mittel (0.2) | UND | es ist angenehm (0.9) | Aktion 4 (0.4) |
Alle anderen Regeln bekämen bei einer UND-Verknüpfung den Erfüllungsgrad null, da mindestens einer der an der jeweiligen Regel beteiligten Terme einen Erfüllungsgrad null, also unwahr, hat. Regeln, die entweder für die Entscheidung unwichtig sind, oder die nie eintreffen, müssen bei der Erstellung des Regelwerkes nicht berücksichtigt werden. So könnte die Regel 9 in Deutschland entfallen, da es hier nie vorkommt, daß es den ganzen Tag überwiegend heiß ist und dabei stark regnet (dieses scheint eher in den tropischen Regionen vorzukommen).
Das Durchlaufen dieser Regeln und Übersetzung der Eingangs-Fuzzy-Sets mittels der gegebenen Regeln in bewertete Ausgangs-Fuzzy-Sets, nennt man „Inferenz". Alle Regeln, die ein Ergebnis mit einem Erfüllungsgrad größer null haben, müssen anschließend mittels eines mathematischen Bewertungs-schemas, welches die Erfüllungsgrade der einzelnen Ergebnisse berücksichtigt, zu einer scharfen Ausgangsgröße gewandelt werden. Diesen Vorgang nennt man Defuzzyfizierung.
Beim Entwurf einer Fuzzy-Regelung
müssen alle scharfen Eingangsgrößen zunächst in sprachliche
Begriffe, sogenannte „linguistische Variablen", gefasst
werden. Diese werden weiter unterteilt in „linguistische
Terme", die auch als „Fuzzy-Sets bezeichnet werden.
Fuzzy-Sets geben für jeden scharfen Wert einer Eingangsgröße
den dazugehörigen Erfüllungsgrad einer fuzzylogischen Aussage
an. Sie stellen eine „Zugehörigkeitsfunktion" oder
auch „Membershipfunktion" auf. Die
Membershipfunktionen werden in der Praxis mittels grafisch
unterstützten Entwicklungssystemen aufgestellt. Im folgenden
soll dies für die Niederschlagsmenge verdeutlicht werden. Zu
erwarten ist eine Niederschlagsmenge zwischen 0 und 4 ![]() .
Als eindeutig „kaum" würde man Werte um 0
.
Als eindeutig „kaum" würde man Werte um 0 ![]() bezeichnen.
Werte um 2 würde man als „mittel" einstufen und Werte
um 4
bezeichnen.
Werte um 2 würde man als „mittel" einstufen und Werte
um 4![]() würden als „stark" eingestuft.
Die Übergänge dazwischen sind fließend.
würden als „stark" eingestuft.
Die Übergänge dazwischen sind fließend.
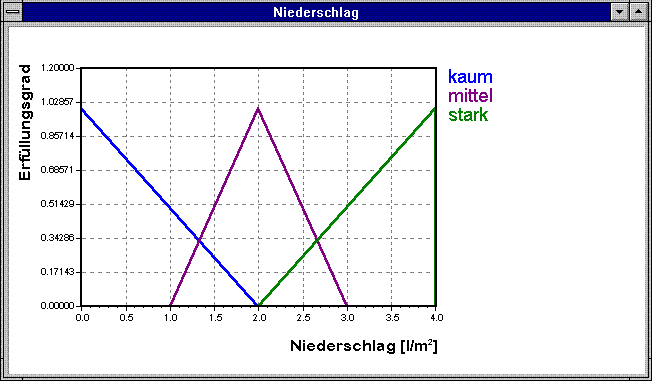
Abbildung 2-1: Linguistische Variable "Niederschlag"
Die zweite linguistische Variable aus Abschnitt 2.2 sähe beispielsweise folgendermaßen aus:
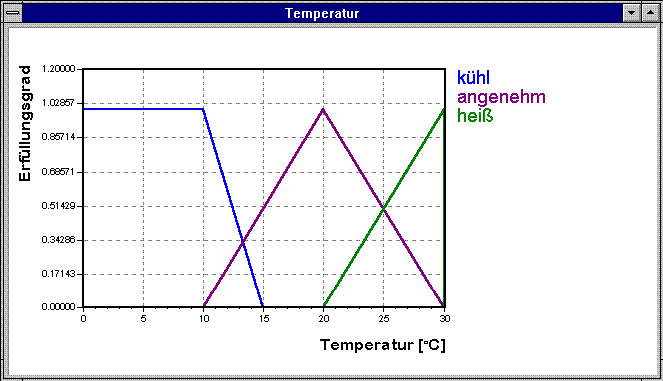
Abbildung 2-2: Linguistische Variable "Temperatur"
Auf der Abszisse sind die scharfen Werte der Eingangsgröße aufgetragen, auf der Ordinate die dazugehörigen Erfüllungsgrade der linguistischen Terme.
An diesem zweiten Beispiel erkennt man, daß die Membershipfunktionen unterschiedliche Formen haben können. Grundlegend gibt es drei verschiedene Formen: Dreieck, Trapez und „Singleton". Ein Singleton ist ein Peak mit dem Wert eins. Singletons werden häufig als Ausgangsgrößen eines Regelwerkes gewählt, da der weitere Rechenaufwand Defuzzyfizierung hierbei recht klein ist.
In einer Regelung werden scharfe Eingangsgrößen über die grafisch erstellten Membershipfunktionen in Erfüllungsgrade fuzzylogischer Aussagen umgerechnet. Diese Erfüllungsgrade werden anschließend im Regelwerk weiterverarbeitet. Das Regelwerk besteht aus einer Sammlung fuzzylogischer Aussagen in Form von WENN (Ausdruck) DANN (Ergebnis). „Ausdruck" kann hierbei ein einzelner linguistischer Term oder eine fuzzylogische Verknüpfung mehrerer linguistischer Terme sein.
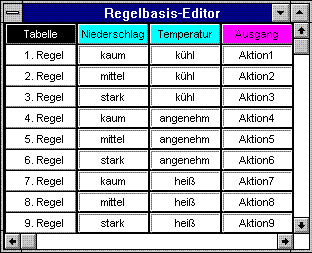
Abbildung 2-3: Beispiel einer Regelbasis
Im abgebildeten Beispiel sind alle möglichen, einfach kombinierten Regeln aufgeführt. In der Praxis sollte man sich auf die benötigten Regeln beschränken.
Für die Verknüpfung zwischen den beiden linguistischen Termen im Ausdruck-Teil der Regeln stehen verschiedene Verknüpfungsoperatoren zur Verfügung. Die gebräuchlichsten sind „UND" und „ODER". Fuzzylogische UND- und ODER-Operatoren haben mit der herkömmlichen, binären Logik nicht sehr viel gemein. Das fuzzylogische UND stellt die Schnittmenge zweier Fuzzy-Sets dar, das fuzzylogische ODER die Vereinigungsmenge zweier Fuzzy-Sets. Abbildung 2-4 stellt diese beiden Verknüpfungen anhand zweier Fuzzy-Sets dar. Die grauen Flächen sind das Ergebnis-Fuzzy-Set der Fuzzy-Verknüpfung.
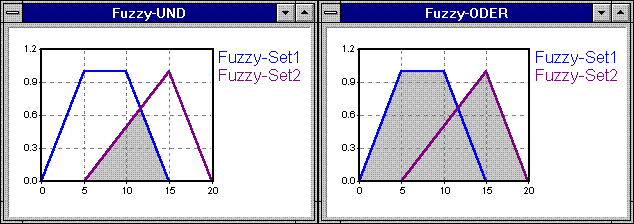
Abbildung 2-4: Die Fuzzy-Verknüpfungen UND und ODER
Der Vorgang, aus bewerteten Eingangs-Fuzzy-Sets über das Regelwerk ein bewertetes Fuzzy-Ausgangs-Set zu erstellen, heißt „Inferenz". Es gibt zwei grundlegende Inferenzschemata - die MAX-MIN-Inferenz und die MAX-PROD-Inferenz. Bei der MAX-MIN-Inferenz werden die Ausgangs-Fuzzy-Sets oberhalb ihres Erfüllungsgrades abgeschnitten. Die Max-PROD-Inferenz staucht die Ausgangs-Fuzzy-Sets in Y-Richtung zusammen, so daß ihr Maximalwert dem Erfüllungsgrad entspricht.
Eine vollständige MAX-MIN-Inferenz der Regel „WENN Fuzzy-Set1 ODER Fuzzy-Set2 DANN Ergebnis" sähe für den Eingangswert 11 folgendermaßen aus:
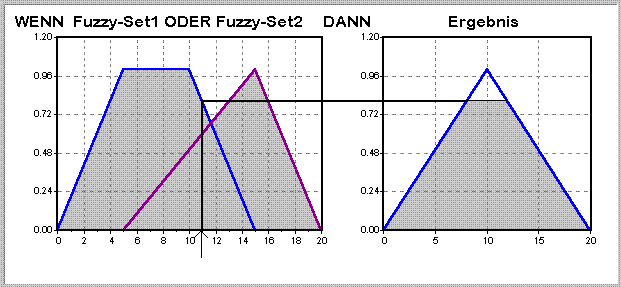
Abbildung 2-5: Beispiel einer MAX-MIN-Inferenz
Eine vollständige MAX-PROD-Inferenz der Regel „WENN Fuzzy-Set1 ODER Fuzzy-Set2 DANN Ergebnis" sähe für den Eingangswert 11 folgendermaßen aus:
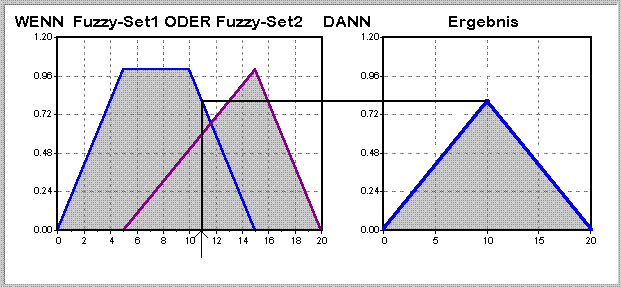
Abbildung 2-6: Beispiel einer MAX-PROD-Inferenz
Bei allen Inferenzmethoden gilt, daß zuerst die Eingangs-Fuzzy-Sets miteinander verknüpft werden. Anschließend wird der aus der Verknüpfung gewonnene Erfüllungsgrad ermittelt und auf das Ergebnis-Fuzzy-Set übertragen. Die Form des Ergebnis-Fuzzy-Sets hängt von der verwendeten Inferenzmethode ab.
Sind alle Regeln durchlaufen und somit alle Ausgangs-Fuzzy-Sets bewertet, so müssen diese mittels Fuzzy-ODER zu einer Gesamt-Fuzzy-Ausgangsmenge zusammengefasst werden. Die entstandene Ausgangs-Fuzzy-Menge muß anschließend wieder zu einem scharfen Ausgangswert gewandelt werden. Dieser Vorgang heißt Defuzzyfizierung. Zur Defuzzyfizierung gibt es verschiedene Methoden. Die Gebräuchlichsten sind Flächenschwerpunkt-Methode, Schwerpunktbildung über Singletons, Linkes Maximum der Fuzzy-Ergebnismenge und Rechtes Maximum der Fuzzy-Ergebnismenge. Die erste der angeführten Methoden fordert dabei den größten Rechenaufwand, zur letzten angeführten Methode hin sinkt dieser ab.
Im folgenden seien die einzelnen Verfahren verdeutlicht.
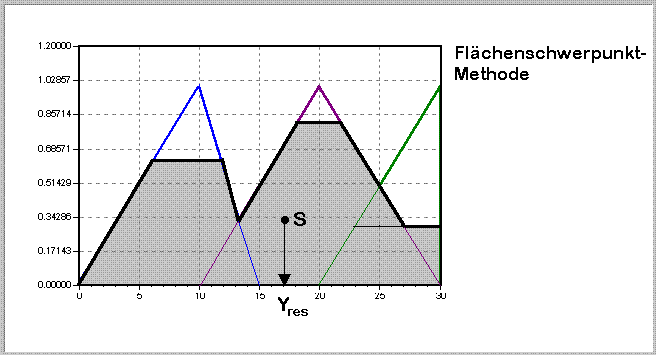
Abbildung 2-7: Flächenschwerpunktmethode
Der Schwerpunkt der Ergebnis-Fuzzy-Set-Fläche wird mathematisch ermittelt. Der zugehörige Abszissenwert gibt die scharfe Ausgangsgröße an.
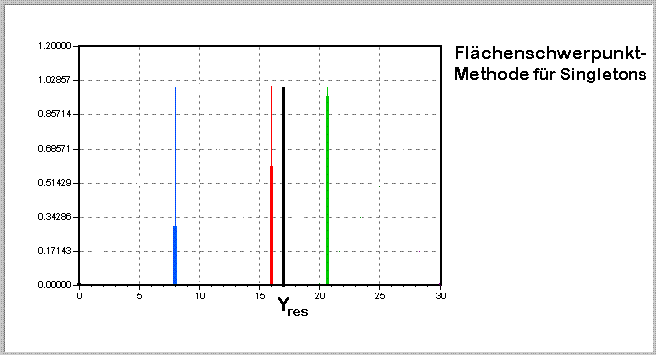
Abbildung 2-8: Flächenschwerpunktmethode für Singletons
Der scharfe Ausgangswert wird über die Summe aller bewerteten Singletons, dividiert durch die Summe aller Erfüllungsgrade, ermittelt.
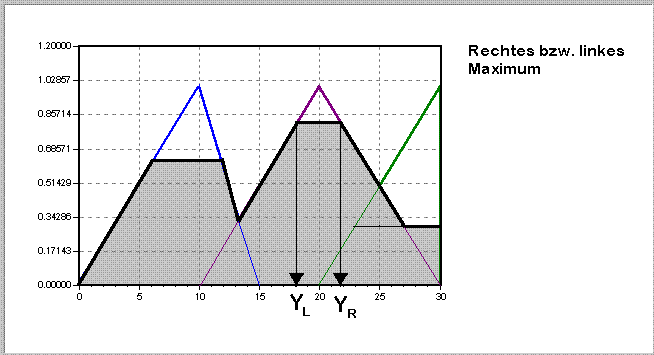
Abbildung 2-9: Rechtes bzw. linkes Maximum der Fuzzy-Ausgangsmenge
Bei der Methode des rechten bzw. linken Maximums der Fuzzy-Ausgangsmenge wird dasjenige Fuzzy-Ausgangs-Set mit dem größten Erfüllungsgrad ausgewählt und der Abszissenpunkt der rechten bzw. linken Begrenzung des Maximums als scharfe Ausgangsgröße bestimmt.
Zusammenfassend sei hier noch einmal ein schematischer Systemüberblick eines Fuzzy-Reglers angegeben.
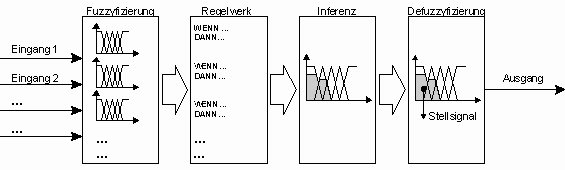
Abbildung 2-10: Systemüberblick eines Fuzzy-Reglers